![李冶[中國古代數學家]](/img/8/2ba/nBnauM3XxgTNzYzN1MDOxUjNxITM4QTMxcTMwADMwAzMxAzLzgzL3MzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg "李冶[中國古代數學家]")
簡介
李冶(1192----1279)，原名李治，號敬齋，金代真定欒城人，曾任鈞州（今河南禹縣）知事，1232年鈞州被蒙古軍所破，遂隱居治學，被元世祖忽必烈聘為翰林學士，僅一年，便辭官回鄉。1248年撰成《測圓海鏡》，其主要目的是說明用天元術列方程的方法。“天元術”與現代代數中的列方程法相類似，“立天元一為某某”，相當於“設x為某某“，可以說是符號代數的嘗試。李冶還有另一步數學著作《益古演段》（1259）也是講解天元術的。
生平
李冶(1192-1279)是中國古代數學家，字仁卿，號敬齋，真定府欒城縣(今河北省欒城縣)人。李冶生於大興(今北京市大興縣)，父親李通為大興府推官．李冶自幼聰敏，喜愛讀書，曾在元氏縣(今河北省元氏縣)求學，對數學和文學都很感興趣．《元朝名臣事略》中說："公(指李冶)幼讀書，手不釋卷，性穎悟，有成人之風．"1230年，李冶在洛陽考中詞賦科進士，任鈞州(今河南禹縣)知事，為官清廉、正直．1232年，鈞州城被蒙古軍隊攻破．李冶不願投降，只好換上平民服裝，北渡黃河避難．
經過一段時間的顛沛流離之後，李冶定居於崞山(今山西崞縣)之桐川．1234年初，金朝終於為蒙古所滅．金朝的滅亡給李冶生活帶來不幸，但由於他不再為官，這在客觀上使他的科學研究有了充分的時間．他在桐川的研究工作是多方面的，包括數學、文學、歷史、天文、哲學、醫學．其中最有價值的工作是對天元術進行了全面總結，寫成數學史上的不朽名著--《測圓海鏡》．他的工作條件是十分艱苦的，不僅居室狹小，而且常常不得溫飽，要為衣食而奔波．但他卻以著書為樂，從不間斷自己的寫作．據《真定府志》記載，李冶"聚書環堵，人所不堪"，但卻"處之裕如也"．他的學生焦養直說他："雖饑寒不能自存，亦不恤也"，在"流離頓挫"中"亦未嘗一日廢其業"．經過多年的艱苦奮鬥，李冶的《測圓海鏡》終於在l248年完搞．它是我國現存最早的一部系統講述天元術的著作．
1251年，李冶的經濟情況有所好轉，他結束了在山西的避難生活，回元氏縣封龍山定居，並收徒講學．1257年在開平(今內蒙古正藍旗)接受忽必烈召見，提出一些進步的政治建議．l259年在封龍山寫成另一部數學著作-一《益古演段》．1265年應忽必烈之聘，去燕京(今北京)擔任翰林學士知制潔同修國史官職，因感到在翰林院思想不自由，第二年辭耿還鄉．李冶是一位多才多藝的學者，除數學外，在文史等方面也深有造詣．他晚年完成的《敬齋古今注》與《泛說》是兩部內容豐富的著作，是他積多年筆記而成的．《泛說》一書已失傳，僅存數條於《敬齋古今注》附錄．他還著有《文集》四十卷與《壁書叢制》十二卷，已佚．1279年，李冶病逝於元氏．李冶在數學上的主要成就是總結並完善了天元術，使之成為中國獨特的半符號代數．這種半符號代數的產生，要比歐洲早三百年左右．他的《測圓海鏡》是天元術的代表作，而《益古演段》則是一本普及天元術的著作．
所謂天元術，就是一種用數學符號列方程的方法，"立天元一為某某"相當於今"設x為某某"是一致的．在中國，列方程的思想可追溯到漢代的《九章算術》，書中用文字敘述的方法建立了二次方程，但沒有明確的未知數概念．到唐代，王孝通已經能列出三次方程，但仍是用文字敘述的，而且尚未掌握列方程的一般方法．經過北宋賈憲、劉益等人的工作，求高次方程正根的問題基本解決了．隨著數學問題的日益複雜，迫切需要一種普遍的建立方程的方法，天元術便在北宋應運而生了、洞淵、石信道等都是天元術的先驅．但直到李冶之前，天元術還是比較幼稚的，記號混亂、複雜，演算煩瑣．例如李冶在東平(今山東省東平縣)得到的一本講天元術的算書中，還不懂得用統一符號表示未知數的不同次冪，它"以十九字識其上下層，曰仙、明、霄、漢、壘、層、高、上、天、人、地、下、低、減、落、逝、泉、暗、鬼．"這就是說，以"人"字表示常數，人以上九字表示未知數的各正數次冪(最高為九次)，入以下九字表示未知數的各負數次冪(最低也是九次)，其運算之繁可見一斑．從稍早於《測圓海鏡》的《鈴經》等書來看，天元術的作用還十分有限．李冶則在前人的基礎上，將天元術改進成一種更簡便而實用的方法．當時，北方出了不少算書，除《鈴經》外，還有《照膽》、《如積釋鎖》、《復軌》等，這無疑為李冶的數學研究提供了條件．特別值得一提的是，他在桐川得到了洞淵的一部算書，內有九客之說，專講勾股容圓問題．此書對他啟發甚大．為了能全面、深入地研究天元術，李冶把勾股容圓(即切圓)問題作為一個系統來研究．他討論了在各種條件下用天元術求圓徑的問題，寫成《測圓海鏡》十二卷，這是他一生中的最大成就．
《測圓海鏡》不僅保留了洞淵九容公式，即9種求直角三角形內切圓直徑的方法，而且給出一批新的求圓徑公式．卷一的"識別雜記"闡明了圓城圖式中各勾股形邊長之間的關係以及它們與圓徑的關係，共六百餘條，每條可看作一個定理(或公式)，這部分內容是對中國古代關於勾股容圓問題的總結．後面各卷的習題，都可以在"識別雜記"的基礎上以天元術為工具推導出來．李冶總結出一套簡明實用的天元術程式，並給出化分式方程為整式方程的方法．他發明了負號和一套先進的小數記法，採用了從零到九的完整數碼．除O以外的數碼古已有之，是籌式的反映．但籌式中遇O空位，沒有符號O．從現存古算書來看，李冶的《測圓海鏡》和秦九韶《數書九章》是較早使用O的兩本書，它們成書的時間相差不過一年．《測圓海鏡》重在列方程，對方程的解法涉及不多．但書中用天元術導出許多高次方程(最高為六次)，給出的根全部準確無誤，可見李冶是掌握高次方程數值解法的．
《測圓海鏡》的成書標誌著天元術成熟，它無疑是當時世界上第一流的數學著作．但由於內容較深，粗知數學的人看不懂．而且當時數學不受重視，所以天元術的傳播速度較慢．李冶清楚地看到這一點，他堅信天元術是解決數學問題的一個有力工具，同時深刻認識到普及天元術的必要性．他在結束避難生活、回元氏縣定居以後，許多人跟他學數學，促使他寫一本深入淺出、便於教學的書，《益古演段》便是在這種情況下寫成的．《測困海鏡》的研究對象是離生活較遠而自成系統的圓城圖式，《益古演段》則把天元術用於解決實際問題，研究對象是日常所見的方、圓面積．李冶大概認識到，天元術是從幾何中產生的．因此，為了使人們理解天元術，就需回顧它與幾何的關係，給代數以幾何解釋，而對二次方程進行幾何解釋是最方便的，於是便選擇了以二次方程為主要內容的《益古集》(11世紀蔣周撰)．正如《四庫全書·益古演段提要》所說："此法(指天元術)雖為諸法之根，然神明變化，不可端倪，學者驟欲通之，茫無門徑之可入．惟因方圓冪積以明之，其理尤屆易見．"李冶是很樂於作這種普及工作的，他在序言中說："使粗知十百者，便得入室啖其文，顧不快哉！"《益古演段》的價值不僅在於普及天元術，理論上也有創新首先，李冶善於用傳統的出入相補原理及各種等量關係來減少題目中的未知數個數，化多元問題為一元問題．其次，李冶在解方程時採用了設輔助未知數的新方法，以簡化運算．
測圓海鏡
《測圓海鏡》是現存最早的一部以天元術為主要內容的著作．天元術雖在北宋已經產生，但直到李冶之前還不成熟，記號混亂、複雜，演算煩瑣，甚至不懂得用統一符號表示未知數的不同次冪．李冶致力於改進天元術，使之簡便而實用．《測圓海鏡》就是他長期研究天元術的成果．
《測圓海鏡》卷一的圓城圖式是全書出發點．該圖以一個直角三角形及其內切圓為基礎，通過若干互相平行或垂直的直線，構成16個直角三角形．書中題目都是已知某些三角形邊長，求圓徑．卷一的“識別雜記”闡明了各勾股形邊長及其與圓徑的關係，共600餘條，每條可看作一個定理或公式，這部分內容是對中國古代勾股容圓問題的總結．卷二到十二為習題，共170題．全書基本上是一個演繹體系，卷一包含了解題所需的基本理論，後面各卷問題的解法均可在此基礎上以天元術為工具推導出來．
李冶的天元術分為三步：首先“立天元一”，這相當於設未知數x；然後尋找兩個等值的且至少有一個含天元的多項式(或分式)；最後把兩個多項式(或分式)連為方程，通過相消，化成標準形式
anxn+an-1xn-1+…+a1x+a0＝0．
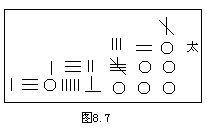
李冶稱方程式為天元式，在《測圓海鏡》中採用由高次冪到低次冪上下排列的順序，式中只標“元”或“太”一個字，元代表一次項，太代表常數項，負係數加一斜線，零係數標數碼○．例如
-x2＋320x－132800＋13056000x-1＝0
和-414x2＋478584＝0
分別寫為圖8．7和圖8．8的形式．下面以卷四第六問為例，用現代符號表出李冶的解題過程．
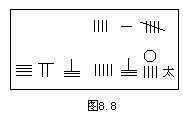李冶
李冶已知：a3＝200，c11＝170．
求：D．
解：由識別雜記，得b。
15＝a3－c11=30．
設半徑為x，則
b11=x＋b15＝x＋30，
a11＝a3-x＝200-x，
a1＝a3＋x＝200＋x．
因為△1∽△11，所以
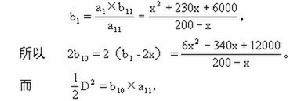李冶所以D2＝2b10×a11=6x2-340x＋12000．
又因為D2＝(2x)2＝4x2，
所以4x2=6x2-340x＋12000．
相消(相當於移項，合併同類項)，得
2x2-340x+12000＝0，
即x2-170x＋6000＝0．
解方程，得
x＝120．
所以D＝2×120＝240．
《測圓海鏡》的理論成果是巨大的．宋代以前，方程理論一直受幾何思維束縛，如常數項只能為正，因為常數項通常是表示面積、體積等幾何量的；方程次數不高於三次，因為超過三次的方程就難於找到幾何解釋了．宋代天元術的產生，標誌著方程理論有了獨立於幾何的傾向，李冶對天元術的總結，則使方程理論基本上擺脫了幾何思維的束縛，實現了程式化．李冶認識到代數計算可以不依賴於幾何，方程的二次項不一定表示面積，三次項也不一定表示體積．他在《測圓海鏡》中改變了傳統的把實(常數項)看作正數的觀念，常數項可正可負．書中用天元術列出許多高次方程，包括三次、四次和六次方程．李冶還處理了分式方程，他是通過方程兩邊同乘一個整式的方法，化分式方程為整式方程的．當方程各項含有公因子xn(n為正整數)時，李冶便令次數最低的項為實，其他各項均降低這一次數．
《測圓海鏡》的成書標誌著天元術成熟，不久以後，王恂、郭守敬(1231—1316)在編《授時曆》時，便用天元術求周天弧度，沙克什則用天元術解決水利工程中的問題，都收到良好效果．元代數學家朱世傑曾說：“以天元演之，明源活法，省功數倍．”以《測圓海鏡》為代表的天元術理論，對後世數學影響很大．李冶死後，天元術經二元術、三元術，迅速發展為四元術，成功地解決了四元高次方程組的建立和求解問題，達到宋元數學的頂峰．
治學態度
李冶作為一個有成就的數學家，在治學態度方面，具有與古往今來的科學家所共有的精神，也有其獨特之點：
1．在極端艱苦的條件下堅持科學研究，從不間斷自己的工作。李冶處在一個動盪不定的時代，特別是棄官隱居以後，從事科學研究的環境是十分艱苦的，常常饑寒至不能自存，但仍處之泰然，以講學著書為樂。對於數學研究，他也是下過苦功的，他在病危時對其子克修說：“測圓海鏡一書，雖九九小數，五常精思致力焉，後世必有知者”。
2．堅持科學真理，不為閒言蜚語所動搖數學研究在當時社會是被輕視的，李冶的工作很少得到當時學者的理解。《測圓海鏡》和《益古演段》兩書，是在他逝世後三十年才得以付印的。
3．善於接受前人知識，取其精華。有人問學於李冶，李冶回答說：“學有三：積之之多不若取之之精，取之之精不若得之之深”。這就是說，要去其糟粕，取其精華，並使它成為自己的東西．
4．反對文章的深奧化和庸俗化，主張文章是為別人，而不是為自己。李冶在《益古演段》序中說：“今之算者，未必有劉（徽）李（淳風）之工，而編心踞見，不肯曉然示人唯務隱互錯揉故為溪滓黯哭，唯恐學者得窺其仿佛也。”他的《益古演段》就是這種主張下的著作。
